PROBLEM
Find the surface area and volume of the composite 3D figure below.
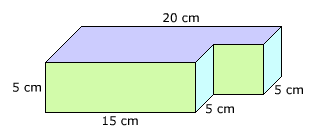
View the composite 3D figure as a right rectangular prism together with a cube, then find any missing lengths in order to calculate the surface area and volume.
A composite 3D figure is a three dimensional figure made up of basic three dimensional figures such as cubes, prisms, pyramids, cylinders, cones, etc.
To find the surface area of a composite 3D figure, add the areas of each geometric figure making up the composite 3D figure.
To find the volume of a composite 3D figure, draw any necessary planes to view the figure as basic three dimensional figures, then:
PROBLEM
Find the surface area and volume of the composite 3D figure below.

View the composite 3D figure as a right rectangular prism together with a cube, then find any missing lengths in order to calculate the surface area and volume.
SURFACE AREA SOLUTION
Note that there are more elegant solutions to calculate the surface area than the one shown below, but the solution shown below illustrates separating a composite 3D figure into basic 3D figures.
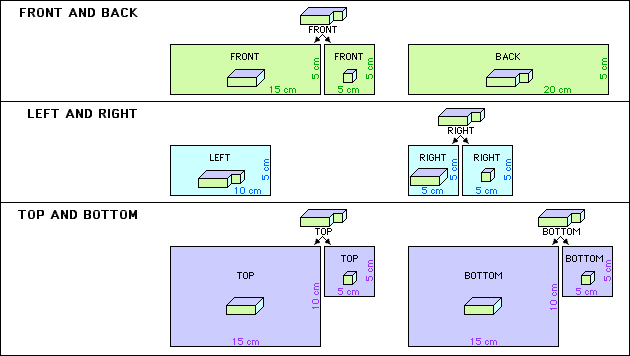
S: Surface area of composite 3D figure.
A: Area.
S = AFRONT + ABACK + ALEFT + ARIGHT + ATOP + ABOTTOM
S = [(15 cm)(5 cm) + (5 cm)(5 cm)] + (20 cm)(5 cm) + (10 cm)(5 cm) + [(5 cm)(5 cm) + (5 cm)(5 cm)] + [(15 cm)(10 cm) + (5 cm)(5 cm)] + [(15 cm)(10 cm) + (5 cm)(5 cm)]
S = 650 cm2
The surface area of the given composite 3D figure is 650 cm2
VOLUME SOLUTION ONE
V: Volume.
Vcomposite 3D figure = Vrectangular right prism + Vcube
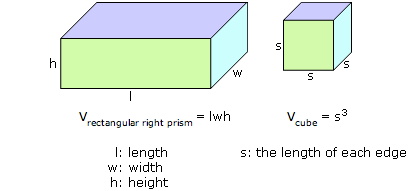
Vcomposite 3D figure = (15 cm)(10 cm)(5 cm) + (5 cm)3
Vcomposite 3D figure = 750 cm3 + 125 cm3
Vcomposite 3D figure = 875 cm3
The volume of the given composite 3D figure is 875 cm3
AREA SOLUTION TWO
Note that there are other similar ways to calculate the volume of the given composite 3D figure. For example rather than viewing the composite 3D figure as a rectangular right prsim together with a cube, it can be viewed as rectangular right prism less a cube.
V: Volume.
Vcomposite 3D figure = Vrectangular right prism - Vcube

Vcomposite 3D figure = (20 cm)(10 cm)(5 cm) - (5 cm)3
Vcomposite 3D figure = 1000 cm3 - 125 cm3
Vcomposite 3D figure = 875 cm3
The volume of the given composite 3D figure is 875 cm3